Bài giảng 30: Phân tích giá trị kỳ dị (Singular Value Decomposition)
(Nếu công thức chưa load được hoặc mờ, các bạn ấn refresh để công thức hiện và rõ nét hơn nhé!)
Các định lý chéo hóa đóng vai trò quan trọng trong nhiều ứng dụng thú vị. Tuy nhiên, như chúng ta đã biết, không phải mọi ma trận đều có thể được phân tích dưới dạng ![]() với
với ![]() là ma trận đường chéo. Tuy nhiên, một phân tích dưới dạng
là ma trận đường chéo. Tuy nhiên, một phân tích dưới dạng ![]() là khả thi đối với mọi ma trận
là khả thi đối với mọi ma trận ![]() bất kỳ! Một phép phân tích đặc biệt thuộc loại này, gọi là phân tích giá trị kỳ dị (singular value decomposition – SVD), là một trong những phép phân tích ma trận hữu ích nhất trong đại số tuyến tính ứng dụng.
bất kỳ! Một phép phân tích đặc biệt thuộc loại này, gọi là phân tích giá trị kỳ dị (singular value decomposition – SVD), là một trong những phép phân tích ma trận hữu ích nhất trong đại số tuyến tính ứng dụng.
Phân tích giá trị kỳ dị dựa trên tính chất sau của phép chéo hóa thông thường, một tính chất có thể được mô phỏng đối với các ma trận hình chữ nhật: Giá trị tuyệt đối của các trị riêng của một ma trận đối xứng ![]() phản ánh mức độ mà
phản ánh mức độ mà ![]() kéo giãn hoặc thu hẹp một số vectơ nhất định (các vectơ riêng). Nếu
kéo giãn hoặc thu hẹp một số vectơ nhất định (các vectơ riêng). Nếu ![]() và
và ![]() , thì:
, thì:
(1) ![]()
Nếu ![]() là trị riêng có độ lớn lớn nhất, thì một vectơ riêng đơn vị tương ứng
là trị riêng có độ lớn lớn nhất, thì một vectơ riêng đơn vị tương ứng ![]() xác định một hướng mà trong đó hiệu ứng kéo giãn của ma trận
xác định một hướng mà trong đó hiệu ứng kéo giãn của ma trận ![]() là lớn nhất. Nói cách khác, độ dài của
là lớn nhất. Nói cách khác, độ dài của ![]() đạt giá trị cực đại khi
đạt giá trị cực đại khi ![]() , và
, và ![]() , theo phương trình (1). Mô tả này về
, theo phương trình (1). Mô tả này về ![]() và
và ![]() cũng có một tương tự đối với các ma trận hình chữ nhật, điều này sẽ dẫn đến phép phân tích giá trị kỳ dị.
cũng có một tương tự đối với các ma trận hình chữ nhật, điều này sẽ dẫn đến phép phân tích giá trị kỳ dị.
Ví dụ 1: Nếu ![]() , thì phép biến đổi tuyến tính
, thì phép biến đổi tuyến tính ![]() sẽ ánh xạ mặt cầu đơn vị
sẽ ánh xạ mặt cầu đơn vị ![]() trong
trong ![]() thành một hình elip trong
thành một hình elip trong ![]() , như được minh họa trong hình 1. Hãy tìm một vectơ đơn vị
, như được minh họa trong hình 1. Hãy tìm một vectơ đơn vị ![]() sao cho độ dài
sao cho độ dài ![]() đạt giá trị lớn nhất, và tính độ dài cực đại này.
đạt giá trị lớn nhất, và tính độ dài cực đại này.

 sang
sang 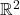 .
.Giải: Đại lượng ![]() đạt giá trị cực đại tại cùng một vectơ
đạt giá trị cực đại tại cùng một vectơ ![]() với
với ![]() , và
, và ![]() thì dễ khảo sát hơn. Ta có:
thì dễ khảo sát hơn. Ta có:
![]()
Ngoài ra, ![]() là một ma trận đối xứng, vì
là một ma trận đối xứng, vì ![]() . Do đó, bài toán trở thành: Tối đa hóa dạng toàn phương
. Do đó, bài toán trở thành: Tối đa hóa dạng toàn phương ![]() với điều kiện
với điều kiện ![]() . Theo định lý 6, giá trị cực đại sẽ là trị riêng lớn nhất
. Theo định lý 6, giá trị cực đại sẽ là trị riêng lớn nhất ![]() của
của ![]() . Giá trị cực đại đó đạt được tại vectơ riêng đơn vị tương ứng với
. Giá trị cực đại đó đạt được tại vectơ riêng đơn vị tương ứng với ![]() của
của ![]() .
.
Với ma trận ![]() trong ví dụ này:
trong ví dụ này:

Các trị riêng của ![]() là:
là: ![]() , và
, và ![]() . Các vectơ riêng đơn vị tương ứng lần lượt là
. Các vectơ riêng đơn vị tương ứng lần lượt là

Do đó, giá trị cực đại của ![]() là 360, đạt được khi
là 360, đạt được khi ![]() , là vectơ đơn vị tương ứng với
, là vectơ đơn vị tương ứng với ![]() . Khi đó:
. Khi đó:

Vì ![]() , nên giá trị lớn nhất của
, nên giá trị lớn nhất của ![]() là
là ![]() .
.
Ví dụ 1 cho thấy hiệu ứng của phép biến đổi ![]() lên mặt cầu đơn vị trong
lên mặt cầu đơn vị trong ![]() liên quan mật thiết đến dạng toàn phương
liên quan mật thiết đến dạng toàn phương ![]() . Thực tế, toàn bộ hành vi hình học của phép biến đổi này được mô tả hoàn toàn bởi dạng toàn phương nói trên.
. Thực tế, toàn bộ hành vi hình học của phép biến đổi này được mô tả hoàn toàn bởi dạng toàn phương nói trên.
Các Giá Trị Kỳ Dị của Ma Trận 
Cho ma trận ![]() kích thước
kích thước ![]() . Khi đó,
. Khi đó, ![]() là ma trận đối xứng và có thể được chéo hóa trực chuẩn.
là ma trận đối xứng và có thể được chéo hóa trực chuẩn.
Gọi ![]() là một cơ sở trực chuẩn của
là một cơ sở trực chuẩn của ![]() , bao gồm các vectơ riêng của
, bao gồm các vectơ riêng của ![]() , và
, và ![]() là các giá trị riêng tương ứng. Khi đó, với mỗi
là các giá trị riêng tương ứng. Khi đó, với mỗi ![]() , ta có:
, ta có:
(2) ![]()
Tức là, các giá trị riêng của ![]() đều không âm (
đều không âm (![]() ). Bằng cách đánh số lại nếu cần, ta có thể giả sử rằng:
). Bằng cách đánh số lại nếu cần, ta có thể giả sử rằng:
![]()
Các giá trị kỳ dị của ![]() là căn bậc hai của các giá trị riêng của
là căn bậc hai của các giá trị riêng của ![]() , ký hiệu là
, ký hiệu là ![]() với
với ![]() . Chúng được sắp xếp theo thứ tự giảm dần
. Chúng được sắp xếp theo thứ tự giảm dần ![]() . Theo công thức (2), các giá trị kỳ dị của
. Theo công thức (2), các giá trị kỳ dị của ![]() cũng chính là độ dài của các vectơ
cũng chính là độ dài của các vectơ ![]() .
.
Ví dụ 2: Cho ma trận ![]() như trong ví dụ 1. Vì các giá trị riêng của
như trong ví dụ 1. Vì các giá trị riêng của ![]() là 360, 90 và 0, nên các giá trị kỳ dị (singular values) của
là 360, 90 và 0, nên các giá trị kỳ dị (singular values) của ![]() là:
là:
![]()
Từ ví dụ 1, ta biết rằng giá trị kỳ dị thứ nhất của ![]() chính là giá trị lớn nhất của
chính là giá trị lớn nhất của ![]() khi
khi ![]() chạy qua tất cả các vectơ đơn vị, và giá trị lớn nhất này đạt được tại vectơ riêng đơn vị
chạy qua tất cả các vectơ đơn vị, và giá trị lớn nhất này đạt được tại vectơ riêng đơn vị ![]() . Định lý 7 chỉ ra rằng giá trị kỳ dị thứ hai của
. Định lý 7 chỉ ra rằng giá trị kỳ dị thứ hai của ![]() là giá trị lớn nhất của
là giá trị lớn nhất của ![]() trên tập tất cả các vectơ đơn vị vuông góc với
trên tập tất cả các vectơ đơn vị vuông góc với ![]() , và giá trị này đạt được tại vectơ riêng đơn vị thứ hai,
, và giá trị này đạt được tại vectơ riêng đơn vị thứ hai, ![]() . Với
. Với ![]() trong ví dụ 1:
trong ví dụ 1:

Điểm này nằm trên trục ngắn của hình elip trong hình 1, tương tự như ![]() nằm trên trục dài. Xem hình 2.
nằm trên trục dài. Xem hình 2.

Hai giá trị kỳ dị đầu tiên của ![]() chính là độ dài của nửa trục dài và nửa trục ngắn của hình elip.
chính là độ dài của nửa trục dài và nửa trục ngắn của hình elip.
Việc ![]() và
và ![]() vuông góc trong hình 2 không phải là ngẫu nhiên, như được chỉ ra trong định lý sau:
vuông góc trong hình 2 không phải là ngẫu nhiên, như được chỉ ra trong định lý sau:
ĐỊNH LÝ 9 Giả sửlà một cơ sở trực chuẩn của
, bao gồm các vector riêng của
, được sắp xếp sao cho các giá trị riêng tương ứng của
thỏa mãn:
và giả sử
có
giá trị kỳ dị khác 0. Khi đó, tập hợp
là một cơ sở trực giao cho cột không gian của
, tức là:
và:
.
Chứng minh Vì ![]() và
và ![]() là trực giao khi
là trực giao khi ![]() ,
,
![]()
Do đó, ![]() là một tập hợp trực giao. Hơn nữa, vì độ dài của các vectơ
là một tập hợp trực giao. Hơn nữa, vì độ dài của các vectơ ![]() là các giá trị kỳ dị của
là các giá trị kỳ dị của ![]() , và vì có
, và vì có ![]() giá trị kỳ dị khác không, nên
giá trị kỳ dị khác không, nên ![]() khi và chỉ khi
khi và chỉ khi ![]() . Vậy các vectơ
. Vậy các vectơ ![]() là độc lập tuyến tính và nằm trong
là độc lập tuyến tính và nằm trong ![]() . Cuối cùng, với mọi
. Cuối cùng, với mọi ![]() thuộc
thuộc ![]() – giả sử
– giả sử ![]() – ta có thể viết
– ta có thể viết ![]() , và
, và
![]()
![]()
Do đó, ![]() thuộc
thuộc ![]() , điều này cho thấy rằng
, điều này cho thấy rằng ![]() là một cơ sở trực giao của
là một cơ sở trực giao của ![]() . Vậy
. Vậy ![]() .
.
Ghi chú số học
Trong một số trường hợp, hạng của ma trận ![]() có thể rất nhạy cảm với những thay đổi nhỏ trong các phần tử của
có thể rất nhạy cảm với những thay đổi nhỏ trong các phần tử của ![]() . Phương pháp hiển nhiên là đếm số cột chốt trong
. Phương pháp hiển nhiên là đếm số cột chốt trong ![]() không hoạt động hiệu quả nếu
không hoạt động hiệu quả nếu ![]() được rút gọn hàng bằng máy tính. Sai số làm tròn thường tạo ra dạng bậc thang với hạng đầy đủ.
được rút gọn hàng bằng máy tính. Sai số làm tròn thường tạo ra dạng bậc thang với hạng đầy đủ.
Trên thực tế, cách đáng tin cậy nhất để ước lượng hạng của một ma trận lớn ![]() là đếm số lượng giá trị kỳ dị khác không. Trong trường hợp này, các giá trị kỳ dị rất nhỏ nhưng khác không được xem như bằng không vì mục đích thực tiễn, và hạng hiệu dụng của ma trận là số lượng các giá trị kỳ dị khác không còn lại sau khi bỏ qua những giá trị nhỏ đó.
là đếm số lượng giá trị kỳ dị khác không. Trong trường hợp này, các giá trị kỳ dị rất nhỏ nhưng khác không được xem như bằng không vì mục đích thực tiễn, và hạng hiệu dụng của ma trận là số lượng các giá trị kỳ dị khác không còn lại sau khi bỏ qua những giá trị nhỏ đó.
- 1 - Bài giảng 23: Xử lý ảnh đa kênh
- 2 - Bài giảng 24: Chéo hóa ma trận đối xứng
- 3 - Bài giảng 25: Phân tích phổ
- 4 - Bài giảng 26: Dạng Toàn Phương
- 5 - Bài giảng 27: Một góc nhìn hình học về các trục chính
- 6 - Bài giảng 28: Phân loại Dạng Toàn Phương
- 7 - Bài giảng 29: Tối ưu hóa có ràng buộc
- 8 - Bài giảng 30: Phân tích giá trị kỳ dị (Singular Value Decomposition)
- 9 - Bài giảng 31: Phân tích giá trị kỳ dị (tiếp theo)
- 10 - Bài giảng 32: Ứng dụng của Phân Tích Giá Trị Kỳ Dị (SVD)
- 11 - Bài giảng 33: Ứng dụng PCA (SVD) trong Xử Lý Ảnh và Thống Kê
- 12 - Bài giảng 34: Trung bình và hiệp phương sai
- 13 - Bàigiảng 35: Phân tích thành phần chính
- 14 - Bài giảng 36: Giảm số chiều của dữ liệu đa biến
